CHAPTER FOUR
Shapes II: Drawing Shapes
In Chapter 2 a shape data type and a function for computing the area of shapes were defined. In the last chapter you learned about
basic graphics programming in Haskell. In this chapter I will define another function of shapes, namely one that converts a shape into a graphics value that can then be drawn in a
graphics window. Conceptually, this function is no different from the area function defined in Chapter 2. In both cases, a shape is turned into some other kind of value; in the
case of area, that value has type Float, and in the case of the function to be defined in this chapter, that value has type Graphic.
In order to perform graphics IO, we need to import the graphics library, as discussed in the last chapter. Additionally, we need to
import the Shape module. Calling our new module Draw, we therefore write:
module Draw ( inchToPixel, pixelToInch, intToFloat,
xWin, yWin, trans, shapeToGraphic, spaceClose
) where
import Shape
import SOEGraphics
where the list of names contains those functions and values, inchToPixel, pixelToInch, etc., that we choose to export from the
module, and that are defined in the remainder of this chapter.
4.1 Dealing With Different Coordinate Systems
Before proceeding, let's define a couple of coercion functions that we will use to convert, or "coerce," the coordinates of a
graphics window into ones that we are more familiar with (and vice versa).
In our discussions of shapes, we have always assumed floating-point numbers for all dimensions, presumably in inches or some similar
dimensional units. But the Graphics Library uses pixel coordinates, so first we need a function to convert from the former to the latter. Let's assume that the floating-point numbers
are in inches, and that there are 100 pixels per inch. Thus, to convert from inches to pixel coordinates, we can apply the following function:
inchToPixel :: Float -> Int
inchToPixel x = round (100 * x)
DETAILS
The value round x is x rounded to the nearest whole number.
 Exercise 4.1 Why is inchToPixel x not defined as 100 * round x? There will also be occasion to coerce in the
other direction:
Exercise 4.1 Why is inchToPixel x not defined as 100 * round x? There will also be occasion to coerce in the
other direction:
pixelToInch :: Int -> Float
pixelToInch n = intToFloat n/100
intToFloat :: Int -> Float
intToFloat n = fromInteger (toInteger n)
DETAILS
The function intToFloat converts an integer into a
floating-point number, but to explain it adequately requires an understanding of Haskell's type classes, which is not covered until
Chapter 12. For now, trust that intToFloat works properly.
 Exercise 4.2 Why is pixelToInch n not defined as intToFloat (n/100)?
Exercise 4.2 Why is pixelToInch n not defined as intToFloat (n/100)?
Also, recall from the previous chapter that the point (0, 0) marks the upper left-hand corner of a graphics window. If we define some
global names for our window size (in pixel coordinates):
xWin, yWin :: Int
xWin = 600
yWin = 500
then the coordinate of the lower right-hand corner is (xWin - 1, yWin - 1). Remember that increasing the x coordinate moves the position to the right, and increasing the y
coordinate moves the position downward.
DETAILS
A type signature may contain more than one name if they all have the same type.
Unfortunately, this graphics window coordinate system is not the same as the one most of us are familiar with. Normally, we
would expect (0, 0) to be in the center of the screen, increasing x to move to the right, and increasing y to move upward. So let's define another coercion function that
translates “our” coordinates into those required by the graphics window:
trans :: Vertex -> Point
trans (x, y) = (xWin2 + inchToPixel x, yWin2 - inchToPixel y)
xWin2, yWin2 :: Int
xWin2 = xWin `div` 2
yWin2 = yWin `div` 2
The values xWin2 and yWin2 are defined at the top-level to prevent them from being recomputed every time trans is
called (although a good compiler may avoid recomputation in any case). As a sanity check on this function, note that:
trans (0, 0) ===> (xWin2, yWin2)
as we would expect. Also note, assuming that inchToPixel and pixelToInch are inverses, that:
trans (pixelToInch xWin2, pixelToInch yWin2) ==> (xWin2 + inchToPixel (pixelToInch xWin2),
yWin2 - inchToPixel (pixelToInch yWin2))
==> (xWin2+xWin2,yWin2-yWin2) ==> (xWin, 0)
which, if you think about it, is also correct.
As a final preliminary task, let us define a function that translates a list of vertices into the points required by a graphics
window:
transEist :: [Vertex] → [Point]
transEist [ ] = [ ]
transEist (p : ps) = trans p : transEist ps
You should convince yourself that this recursive definition achieves the specified task.
Converting Shapes to Graphics
Our goal is to define a function:
shapeToGraphic :: Shape → Graphic
that converts a Shape value into a Graphic value, which can then be drawn using draw. Let's consider each
Shape constructor in turn. The first one, a rectangle, will be the hardest one to convert, but is nonetheless fairly straightforward:
shapeToGraphic (Rectangle s1s2)
= let s12= s1/2 s22= s2/2
in polygon (transList
[(-s12, -s22),(-s12,s22),(s12, s22),(s12, -s22)])
Note the use of transEist to translate the four coordinates of a rectangle centered over the origin to the coordinates needed
by the graphics window.
Converting an ellipse is even more straightforward:
shapeToGraphic (Ellipse r1 r2)
= ellipse (trans (-r1,
-r2)) (trans (r1,
r2))
A right triangle is handled similarly to a rectangle:
shapeToGraphic (RtTriangle s1 s2)
= polygon (transList [(0, 0), (s1, 0), (0, s2)])
And a polygon simply requires translating the vertices:
shapeToGraphic (Polygon vts) = polygon (transList vts)
Collecting the pieces, we arrive at:
shapeToGraphic :: Shape → Graphic shapeToGraphic (Rectangle s1 s2)
= let s12 = s1/2 s22 = s2/2
in polygon
(transList [(-s12,
-s22), (-s12, s22),
(s12, s22), (s12,
-s22)])
shapeToGraphic (Ellipse r1 r2)
= ellipse (trans (-r1,
-r2)) (trans (r1, r2)) shapeToGraphic (RtTriangle s1
s2)
= polygon (transEist [(0, 0), (s1, 0), (0, s2)])
shapeToGraphic (Polygon vts)
= polygon (transEist vts)
4.3 Some Examples
For some examples, let's start by creating a variety of shapes: sh1, sh2, sh3, sh4 :: Shape
sh1 = Rectangle 3 2
sh2 = Ellipse 1 1.5
sh3 = RtTriangle 3 2
sh4 = Polygon [(-2.5, 2.5), (-1.5, 2.0), (-1.1, 0.2),
(-1.7, -1.0), (-3.0, 0)]
We can color and draw shapes one by one by doing something as simple as:
main0
= runGraphics (
do w ← openWindow “drawing Shapes” (xWin, yWin)
drawIn Window w (withColor Red (shapeToGraphic shl)) drawInWindow w (withColor Blue (shapeToGraphic sh2)) spaceClose
w
)
which draws a red rectangle and a blue ellipse centered on the screen.
To make things more convenient, however, let's define a function that draws a whole list of color/shape pairs:
type ColoredShapes = [(Color, Shape)] shs ::
ColoredShapes
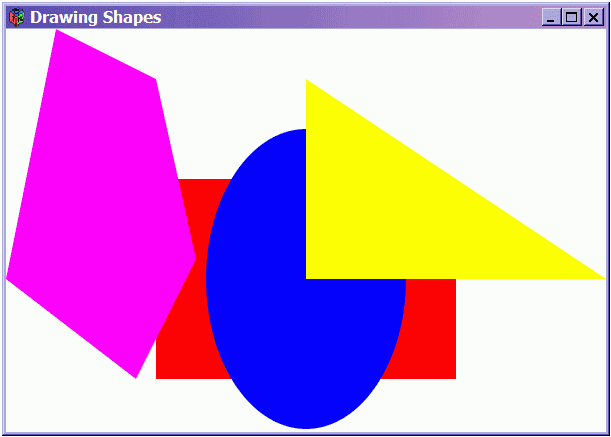
shs = [(Red, shl), (Blue, sh2), (Yellow, sh3), (Magenta, sh4)]
Such a function is simple to define:
drawShapes :: Window → ColoredShapes → IO () drawShapes w [
]
= return () drawShapes w
((c,s) : cs)
= do drawInWindow w (withColor c
(shapeToGraphic s))drawShapes w
cs
and can be used like this:
main1
= runGraphics (
do w ← openWindow “Drawing Shapes” (xWin, yWin)
drawShapes w shs spaceClose w
)
A snapshot of main1 is shown in Fig. 4.1, although the colors have been
Figure 4.1 : Some Colored Shapes (converted to grey tones)
converted to grey tones (as they have been for all of the figures in this text).
4.4 In Retrospect
One might wonder why we bothered to define a function to draw Shape values in the first place, when using the primitive
graphics operations directly, as described in the previous chapter, seems almost as good. In particular, it seems that we could easily define new IO functions for each of the shapes
that we are interested in drawing, and even have these functions take floating-point values as parameters. In other words, something like this:
drawRectangle :: Side → Side → IO () drawEllipse :: Radius
→ Radius → IO () drawRtTriangle :: Side → Side → IO
() drawPolygon :: [Vertex] → IO ()
type Radius = Float type Side = Float
type Vertex = (Float, Float)
indeed, this is possible, and you may wish to define these functions on your own as an exercise.
However, there are a couple of good reasons for doing things “indi-rectly'' using the Shape data type as we have in this
chapter. First, Shape values are ``transparent.'' That is, one can pattern-match against them to learn what their insides look like. For example, we can determine the side
lengths of a rectangle, the radii of an ellipse, and so on. In contrast, a value of type IO () (i.e., an action) is completely
``opaque''; the only thing you can do with it is execute it.
To see the importance of this, suppose I want to do more than one thing with a shape, such as draw it and also compute its area. Then
I am better off having a transparent value representing it, to which I can apply a draw function and an area function independently. And if later I decide to define a new operation on
Shapes - such as a function to compute the perimeter, which we will do in Chapter 6 - then I am in good shape (pardon the pun). Doing all of this with opaque values would be much
more cumbersome.
A second (and related) advantage of our indirect approach will become evident in Chapter 8, where we will define a new data type
called Region that captures ways to combine shapes in interesting ways - such
as taking their union and intersection - and ways to transform them as well - such as scaling and translating them. Having the
Region data type be transparent will be especially useful, not just because we will want to do more than one thing with them as argued above, but because regions will be able to
share subregions. This is not as easily done with opaque values.
 Exercise 4.1 Why is inchToPixel x not defined as 100 * round x? There will also be occasion to coerce in the
other direction:
Exercise 4.1 Why is inchToPixel x not defined as 100 * round x? There will also be occasion to coerce in the
other direction:
 Exercise 4.2 Why is pixelToInch n not defined as intToFloat (n/100)?
Exercise 4.2 Why is pixelToInch n not defined as intToFloat (n/100)?