In this chapter simple graphics programming in Haskell will be explained. Graphics in Haskell is consistent with the notion of computation via calculation, although it is special enough to warrant the use of special terminology and notation. In the next chapter we will use the techniques learned here to draw in a graphics window the geometric shapes defined in the last chapter. The ideas developed in this chapter will be put into a module called SimpleGraphics:

module SimpleGraphics where

There are many predefined functions and data types in Haskell, so many, in fact, that they demand some organization. Entities that are deemed essential to defining the fundamental nature of Haskell are contained in what is called the Standard Prelude, a collection of modules defining various categories of functionality. Entities that are deemed useful but not essential are contained in one of several Standard Libraries, also a collection of modules. The entire Standard Prelude is automatically imported into every program that you write, whereas the Standard Libraries need to be imported module-by-module.

Unfortunately, there is no standard graphics library for Haskell yet, although there is one in popular use on Windows machines called Graphics. The basic graphics functionality that we will use is defined in a library called SOEGraphics, which is very similar to Graphics but is guaranteed to work with this textbook, whereas the Graphics library may evolve over time. To use SOEGraphics, it must be imported into the module that is using it, as follows:

import SOEGraphics

Graphics is a special case of input/output (IO) processing in Haskell, and thus I will begin with a discussion of this more general idea.

The Haskell Report defines the result of a program as the value of the name main in the module Main. On the other hand, the Hugs implementation of Haskell allows you to type whatever expression you wish to the Hugs prompt, and it will evaluate it for you. But in either case, the Haskell system "executes a program" by evaluating an expression, which (for a well-behaved program) eventually yields a value. The system must then display that value on your computer screen in some way that makes sense to you. Most systems will try to display the result in the same way that you would type it in as part of a program. So an integer is printed as an integer, a string as a string, a list as a list, and so on. I will refer to the area of the computer screen where this result is printed as the standard output area, which may vary from one implementation to another.

But what if a program is intended to write to a file or print a file on a printer or, the main topic of this chapter, draw a picture in a graphics window? These are examples of output, and there are related questions about input. For example, how does a program receive input from a keyboard or a mouse?

In general, how does Haskell's "expression-oriented" notion of "computation by calculation" accommodate these various kinds of input and output?

The answer is fairly simple: In Haskell, there is a special kind of value called an action. When a Haskell system evaluates an expression that yields an action, it knows not to try to display the result in the standard output area, but rather to "take the appropriate action". There are primitive actions - such as writing a single character to a file or receiving a single character from the keyboard - as well as compound actions - such as printing an entire string to a file. Haskell expressions that evaluate to actions are commonly called commands, because they command the Haskell system to perform some kind of action. Haskell functions that yield actions when they are applied are also commonly called commands.

Commands are still just expressions, of course, and some commands return a value for subsequent use by the program: keyboard input, for instance. A command that returns a value of type T has type IO T; if no useful value is returned the command has type IO (). The simplest example of a command is return x, which for a value x :: T immediately returns x and has type IO T.

Remember that all expressions in Haskell must be well-typed before a program is run, so a Haskell system knows ahead of time, by looking at the type, that it is evaluating a command, and is thus ready to “take action”.

To make these ideas clearer, let's consider a few examples. A very useful command is the putStr command, which prints a string argument to the standard output area, and has type String -> IO (). The () simply indicates that there is no useful result returned from this action; its sole purpose is to print its argument to the standard output area. So the program:

module Main where
main = putStr "Hello World\n"

do writeFile "testFile.txt" "Hello File System"
   putStr "Hello World\n"

So far we have only used actions having type IO () (i.e., output actions). But what about input? As above, we will consider input from both the user and the file system.

To get a line of input from the user (which will be typed in the standard input area of the computer screen, usually the same as the standard output area) we can use the function:

getLine :: IO String

Suppose, for example, that we wish to read a line of input using this function, and then write that line (a string) to a file. To do this we write the compound command:

do s <- getLine
  writeFile "testFile.txt" s

Note the syntax for binding s to the result of executing the getLine command; because the type of getLine is IO String, the type of s is String. Its value is then used in the next line as an argument to the writeFile command.

Similarly, we can read the entire contents of a file using the command readFile :: FilePath -> IO String. For example:

do s <- readFile "testFile.txt"
   putStr s

There are many other commands available for file, system, and user IO, some in the Standard Prelude, and some in various libraries (such as IO, Directory, System and Time). I will not discuss any of these here; rather, in the next section I will concentrate on graphics IO.

Before that, however, I want to emphasize that, despite the special do syntax, Haskell's IO commands are no different in status from any other Haskell function or value. For example, it is possible to create a list of actions, such as:

actionList = [putStr "Hello World\n",
              writeFile "testFile.txt" "Hello File System",
              putStr "File successfully written."]

sequence_ :: [IO a] -> IO ()

main = sequence_ actionList

Before I give you a more interesting example of this idea, I will tell you a secret (more secrets will be revealed later in the text):

Now back to the example. From the function putChar :: Char → IO (),which prints a single character to the standard output area, we can define the function putStr used earlier, which prints an entire string. To do this, let's first define a function that converts a list of characters (i.e., a string) into a list of IO actions:

putCharList :: String -> [IO  ()]
putCharList [] = []
putCharList (c:cs) = putChar c : putCharList cs

putStr :: String -> IO ()
putStr s = sequence_ (putCharList s) 

IO processing in Haskell is consistent with everything you have learned about programming with expressions and reasoning through calculation, although that may not be completely obvious yet. Indeed, it turns out that a do expression is just syntax for a more primitive way of combining actions using functions. This secret will be revealed in full in Chapter 18.

Let's now look at the particulars of graphics IO. Graphics commands are no different in concept from those discussed earlier. However, there is no "standard graphics area" on which to draw things. Instead, we must create a fresh graphics window. Furthermore, because we may wish to create several such windows, we need a way to distinguish them once they are created, in order to specify in which window to draw at some particular point in a program. Haskell accomplishes this by returning a unique value of type Window at the time we create a window.

To see this concretely, let's look at the type of the openWindow command that (you guessed it) opens a window:

openWindow :: Title -> Size -> IO Window
type Title = String
type Size = (Int, Int) 

The Title is a string displayed in the title bar of the new graphics window, and Size represents the size of the window as a pair of numbers indicating the width and height in pixel coordinates. A pixel is the smallest dot that can be displayed on a computer screen; usually 100 or so pixels can be lined up along one inch. The Window that returns from a call to openWindow is used in subsequent graphics commands to tell the computer within which window to perform its action. In other words, every call to openWindow creates a new, unique window, and the Window value provides a way to distinguish between them in the rest of the program.

Let's write our first graphics program:

main0
  = runGraphics (
    do w <- openWindow "My First Graphics Program" (300, 300)
       drawInWindow w (text (100, 200) "Hello Graphics World")
       k <- getKey w
       closeWindow w
    )

It's not hard to guess what this program does: A 300 × 300-pixel graphics window is opened, a greeting message is displayed in it, and the window remains open until the user types a character on the keyboard. The following five new functions are introduced by this example:

• runGraphics :: IO () -> IO () runs a graphics “action”. This is needed because of special operating system tasks that need to be set up to perform graphics IO.
• drawInWindow :: Window -> Graphic -> IO () draws a given Graphic value on a given Window.
• text :: Point -> String -> Graphic creates a Graphic value consisting of a String whose lower left-hand corner is at the location specified by the Point argument, in pixel coodinates:

  type Point = (Int, Int)
  

• getKey :: Window -> IO () waits for the user to press (and release) a key on the keyboard. In the above example getKey is used to prevent the window from closing before the user has a chance to read what's on the screen.
• closeWindow :: Window -> IO () closes the specified window.

You should know enough about IO at this point that these descriptions are sufficient to fully understand the sample program given above, except for one other detail: (0, 0) is the location of the upper left-hand corner of the graphics window. As the x coordinate increases, the position moves to the right, and as the y coordinate increases, the position moves downward. Thus, in the above program, the bottom right-hand corner of the graphics window is at coordinate (299, 299). I will have more to say about this in the next chapter.

For convenience, I will define the following command, which also demonstrates how to write a loop using command sequencing:

spaceClose :: Window -> IO ()
spaceClose w
  = do k <- getKey w
       if k == ' '
          then closeWindow w
          else spaceClose w

Note that spaceClose is defined recursively, and it is precisely the recursion that achieves the desired looping behavior. This command reads a keystroke and sees if it is the space character (' '). If it is, the window is closed and the command is finished; if it is not, then the process is repeated. Because spaceClose w has type IO (), we can use it in a do expression like this:

main1
  = runGraphics (
    do w <- openWindow
              "My First Graphics Program" (300, 300)
       drawInWindow w (text (100, 200) "Hello Graphics World")
       spaceClose w
    )

We have seen that the function text returns a Graphic value, and we used the function draw to turn that into an action. As it turns out, there are other functions besides text that create Graphic values, in particular ones for drawing certain kinds of geometric shapes:

ellipse :: Point -> Point -> Graphic
shearEllipse :: Point -> Point -> Point -> Graphic
line :: Point -> Point -> Graphic
polyline :: [Point] -> Graphic
polygon :: [Point] -> Graphic
polyBezier :: [Point] -> Graphic 

1. ellipse p1 p2 draws an ellipse that just fits into the rectangle whose upper left-hand vertex is at point p1 and whose lower right-hand vertex is at point p2, using the graphics window coordinate system described earlier.
2. shearEllipse p1 p2 p3 draws an ellipse that just fits into the parallelogram formed by the vertices p1, p2 and p3.
3. line p1 p2 draws a straight line between points p1 and p2.
4. polygon pts draws a closed polygon with vertices pts. The last point is connected back to the first, and thus the polygon can be filled with a color.
5. polyline pts connects each pair of successive points with a straight line, but does not connect the last point back to the first; thus it cannot be filled with a color.
6. polyBezier is like polyline, but uses Bezier curves to connect successive points, rather than straight lines.

If we draw figures and lines using the above primitive functions, the figures and lines will be white by default. To make the colors more interesting, we can use the graphics library function:

withColor :: Color -> Graphic -> Graphic
data Color = Black | Blue | Green | Cyan
           | Red | Magenta | Yellow | White

As a simple example, here is a program that draws a red ellipse and a blue outline of a rectangle.

pic1 = withColor Red
         (ellipse (150, 150) (300, 200))
pic2 = withColor Blue
         (polyline [(100, 50), (200, 50),
                    (200, 250), (100, 250), (100, 50)])
main2
  = runGraphics (
    do w <- openWindow
                 "Some Graphics Figures" (300, 300)
       drawInWindow w pic1
       drawInWindow w pic2
       spaceClose w
    ) 

For a more interesting example, let's draw a simple fractal image. A fractal is a mathematical structure that repeats itself infinitely often in successively finer detail (Barnsle, 1993). Using fractals is a popular method to simulate natural phenomena like skylines, leaves, and snowflakes. I am sure you have seen them in many computer-generated pictures found in calendars, animated movies, among others. A skyline, for example, has the property that as you “zoom in” on it, it looks approximately the same at each level of detail. Whereas this detail is somewhat random for skylines, for crystalline structures such as a snowflake, it is very regular. Both can be modelled using fractals.

The mathematics of fractals is beyond the scope of this textbook, but there are some simple fractal images that are pleasing to the eye yet very easy to describe and draw. One such image is called Sierpinski's Triangle, which can be described via successive drawings of a triangle (Fig. 3.1). The first drawing is a single triangle. The second drawing subdivides the first triangle into three triangles, each one-half the original in both length and height. The third drawing subdivides each of the triangles in the second drawing in a similar way. Now imagine doing this ad infinitum, and there you have Sierpinski's Triangle.

Of course, we cannot actually show this infinitely-dense triangle in a graphics window, because we are limited by pixel size (and our eyes would not be sharp enough to see the details). So to draw Sierpinski's Triangle we will stop subdividing the triangles when we reach some predetermined image size, and then just draw each tiny triangle completely at that point.

First I will define a function fillTri that draws a blue-filled triangle, given x and y coordinates and a size (all in pixel coordinates):

fillTri :: Window -> Int -> Int -> Int -> IO ()
fillTri w x y size
  = drawInWindow w (withColor Blue
      (polygon [(x, y), (x + size, y), (x, y - size), (x, y)]))

The rest of the algorithm is really very easy (and elegant), and is presented in one fell swoop:

minSize :: Int
minSize = 8

sierpinskiTri :: Window -> Int -> Int -> Int -> IO ()
sierpinskiTri w x y size
  = if size <= minSize
    then fillTri w x y size
    else let size2 = size `div` 2
      in do sierpinskiTri w  x  y        size2
            sierpinskiTri w  x (y-size2) size2
            sierpinskiTri w (x+size2)  y size2

Using sierpinskiTri is easy enough; the only trickery is to use a number that is a power of two for the initial size, to make the subdivisions look most uniform by avoiding rounding errors.

main3
  = runGraphics (
    do w <- openWindow "Sierpinski's Triangle" (400,400)
       sierpinskiTri w 50 300 256
       spaceClose w
    )

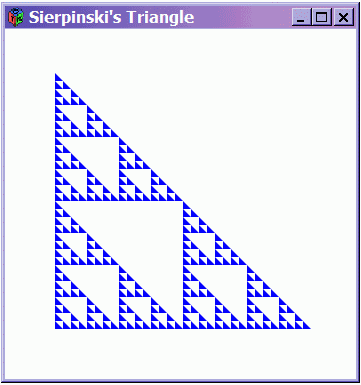
I have shown this example primarily to illustrate how one can use the various graphics primitives in interesting ways. But ultimately we are trying to build higher-level ways to do this, starting with the ability to draw values of type Shape defined in Chapter 2. We will discuss this in the next chapter.