In the previous chapter you learned quite a few techniques for problem solving via calculation in Haskell. It's time now to apply these ideas to a larger example, which will require learning even more problem-solving skills and Haskell language features.
Our job will be to design a simple module of geometric shapes, that is, a collection of functions and data types for computing with geometric shapes such as circles, squares, triangles, and others. Users of this module will be able to create new instances of geometric shapes and compute their areas. You will learn lots of new things in building this module, including how to design your own data types. Then in Chapter 4 we will extend this functionality with the ability to draw geometric shapes, and in Chapter 6 compute their perimeters.
In the description above I refer to the end product as a module, through which a user has access to certain well-defined functionalities. A module can be seen as a way to conveniently wrap up an application in such a way that only the functionality intended for the end-user is visible; everything else needed to implement the system is effectively hidden.
In Haskell we can create a module named Shape in the following way:
module Shape (...) where ... body_of_module...
The "(...)" after the name Shape will ultimately be a list of names of the functions and data types that the end-user is intended to use, and is sometimes called the interface to a module. At the end of this chapter we will fill in the details of the interface once we know what they should be. The ...body_of_module... is of course where we will place all the code developed in this chapter.
Module names must always be capitalized (just like type names).
A user of our shape module can later import it into a module that he or she is constructing, by writing:
import Shape
Indeed, we will do exactly this in later chapters where new modules will be created in which users will be able to draw shapes, compute their perimeters, combine them into larger “regions”, color them, scale them, and place them on a “virtual desktop”. This desktop will be displayed on your computer screen, and will be designed in such a way that regions will rise to the surface of the desktop when they are clicked, just like windows do in a windows-based user-interface.
Our first job will be to design a single data type to represent all of the possible geometric shapes of interest to us. Aside from the fact that this is intuitively appealing, there are several pragmatic reasons for doing so. For example, in Section 1.4.2 we saw a function for computing the area of a circle, and later a function for computing the area of a square. If we were to define functions for computing the areas of, say, n different shapes, we would end up with n functions, each with a different name. Similarly, we would have n functions for drawing shapes and n functions for computing their perimeters. In contrast, if we had a single data type that captured all of the geometric shapes, we could (hopefully) define a single function for each of these tasks.
In Haskell, new data types such as this are defined using a data declaration:
data Shape = Circle Float
| Square Float
This declaration can be read: “There are two kinds of Shapes: a circle of the form Circle r where r is a radius of type Float, and a square of the form Square s where s is the length (also of type Float) of one side”. Because Circle and Square construct new values in this data type, they are called constructors.
All constructors in a data declaration must be capitalized. In this way they are syntactically distinguished from ordinary functions. This distinction is useful because only constructors can be used in the pattern matching that is part of a function definition, as will be described shortly.
Of course, there are more shapes than just circles and squares. And to complicate matters, squares are really rectangles, rectangles are really parallelograms, and parallelograms are just quadrilaterals (4-sided polygons). And, there are (right, equilateral, and isosceles) triangles, trapezoids, pentagons, hexagons, etc. Do we really want representations for all of them? If not, which ones do we choose? This is a difficult design decision that is dependent on the eventual use of the data type, which may be difficult to predict.
For mostly pedagogical purposes, let's settle on the following definition:
data Shape = Rectangle Float Float
| Ellipse Float Float
| RtTriangle Float Float
| Polygon [(Float, Float)]
deriving Show
The phrase “deriving Show” is a way to tell the Haskell system that you are interested in printing out values of the data type that you are defining. Exactly how this is accomplished will be described in a later chapter.
This declaration defines a new data type called Shape in which:
- Rectangle s1 s2 is a rectangle with sides s1 and s2, both floating-point numbers.
- Ellipse r1 r2 is an ellipse with radii r1 and r2, both floating-point numbers.
- RtTriangle s1 s2 is a right triangle with sides of length s1 and s2, both floating-point numbers.
- Polygon [v1, v2, ... , vn] is an n-sided polygon whose vertices are v1 through vn, each vertex being represented by a pair (x, y) of floating-point coordinates on a Cartesian plane. (Recall that (Float, Float) is the type of pairs of floating-point numbers; for example (1.0, pi) :: (Float, Float) ).
One unfortunate aspect of this definition is that floating-point numbers are used to represent several different quantities, a fact only evident in the documentation of the code (such as we have written above). One way to improve on this is to create new names for the various uses of floating-point numbers, which in Haskell can be achieved using a type declaration:
data Shape = Rectangle Side Side
| Ellipse Radius Radius
| RtTriangle Side Side
| Polygon [Vertex]
deriving Show
type Radius = Float
type Side = Float
type Vertex = (Float, Float)
Here the Shape declaration is really the same as before, except that we've used different names for the “constituent types”, and the type declarations telI us what they really are. It is important to realize that, although a data declaration creates a completely new data type, a type declaration does not: it simply creates a new name for an existing type. Indeed, these are called type synonyms because the new name is just a synonym for the old one. The result is “self-documenting”, and arguably easier to read.
This change can also be seen as another application of the abstraction principle. Note, for example, that if we decide to represent sides as double-precision floating-point numbers (which in Haskell have type Double), we could just change a single line:
type Side = Doubleno matter how often we used the name Side. This is a good thing.
Returning to the design issue of deciding which shapes to choose for this data type, you might object to the fact that to create a square with side s you must now write something like Rectangle s s. It is easy to remedy this situation, however, by defining a function square as:
square s = Rectangle s s
Similarly, a circle function can be defined by:
circle r = Ellipse r r
But, you might point out, with the Polygon constructor we can create polygons with an arbitrary number of sides, each with an arbitrary length, so why include the special cases of rectangle and right triangle? In other words, why not just define functions rectangle and rtTriangle in terms of Polygon? Good question! One answer, as mentioned earlier, is in the interest of pedagogy: I am trying to illustrate a variety of programming techniques. Another answer is that the algorithms for computing the areas of rectangles and right triangles are simpler than the algorithm for computing the area of a general polygon. A final answer is that there may be lower-level graphics commands, say, that are more efficient at drawing rectangles and/or right triangles than general polygons. In any case, let's proceed with our design and investigate its consequences later.
 Exercise 2.1
Exercise 2.1Define functions rectangle and rtTriangle in terms of Polygon.
 Exercise 2.2
Exercise 2.2Define a function regularPolygon :: Int -> Side -> Shape such that regularPolygon n s is a regular polygon with n sides, each of length s. (Hint: Consider using some of Haskell's trigonometric functions, such as sin :: Float -> Float, cos :: Float -> Float, and tan :: Float -> Float).
Returning to the problem in Section 1.4.2 of computing areas, we will define a function:
area :: Shape -> Floatby defining its behavior on each of the Shape constructors. We know how to do this for a rectangle:
area (Rectangle s1 s2) = s1 * s2And the area of a right triangle is just as easy:
area (RtTriangle s1 s2) = s1 * s2 / 2
Before proceeding, note that this way of writing function definitions - by pattern matching on the arguments - is just like the way we defined the function listSum in Section 1.4.3. There, listSum was defined by its behavior on the two constructors in the list data types, [ ] and (:). In the case of the Shape data type, we happen to have four constructors to consider instead of two.
Moving on, a standard geometry text tells us that the area of an ellipse with radii r1 and r2 is just π r1 r2. It is easy to see that this reduces to πr2 for a circle. Translated into Haskell, this becomes:
area (Ellipse r1 r2) = pi * r1 * r2
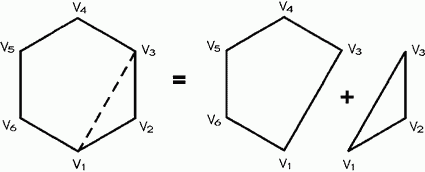
What about the area of a general polygon? If the polygon is convex (meaning that all of its interior angles are less than 180°), its area can be computed fairly simply as follows (the case of concave polygons will be an exercise):
1. Compute the area of the triangle formed by the first three vertices of the polygon.
2. Delete the second vertex, forming a new polygon.
3. If there are at least three vertices in the new polygon, repeat this procedure, returning as the total area the sum of the areas of the individual triangles.
The intuition for this algorithm is shown pictorially in Fig. 2.1; it is another example of solving a problem by solving a smaller problem first, which at least slightly reduces the size of the larger one.
Although we haven't yet decided how to compute the area of a general triangle, we can write out the above algorithm in Haskell as follows:
area (Polygon ( v1 : v2 : v3 : vs)) = triArea v1 v2 v3 + area (Polygon (v1 : v3 : vs)) area (Polygon _) = 0
The first line above is an example of a nested pattern; that is, the pattern (v1 : v2 : v3 : vs) is nested within the pattern Polygon....
The second equation uses an “underscore” character “_” as a pattern. This is called a wildcard pattern, and matches any argument. When more than one equation is used to define a function, Haskell will try them in the order that they appear. So in the case of area, an attempt is first made to match a list containing at least three elements. If that fails, then the second equation is tried, which of course succeeds immediately, yielding the value 0.
This version of the algorithm has a more “declarative” feel than the description given earlier and can be read: “The area of a (convex) polygon is the area of the triangle formed by its first three vertices, plus the area of the polygon resulting from deleting the second vertex”. In general, we will try to write declarative definitions such as this directly.
However, note in the recursive call to area that the polygon is “reconstructed” using the Polygon constructor; so the polygon is taken apart and then put back together, so to speak, on each recursive call. Also note that the first vertex never disappears; it is always part of the reconstruction. We can avoid these slight inefficiencies by defining an auxiliary function polyArea that computes the area directly from a list of vertices, as follows:
area (Polygon (v1 : vs)) = polyArea vs
where polyArea :: [Vertex] -> Float
polyArea (v2 : v3 : vs') = triArea v1 v2 v3
+ polyArea (v3 : vs')
polyArea _ = 0
Note the use of a where expression. For the most part you can consider exp where ...equations... to be equivalent to let ...equations... in exp. The only difference is that a where expression is only allowed at the top level of a function definition, where its visibility rules are slightly different (see the Haskell Report for details).
What about triArea? Fortunately, there is a single formula for the area of an arbitrary triangle with sides of
lengths a, b and c, due to Heron:
A = √s(s - a)(s - b)(s - c) where s = ½(a + b + c); or, in Haskell:
triArea :: Vertex -> Vertex -> Vertex -> Float
triArea v1 v2 v3 = let a = distBetween v1 v2
b = distBetween v2 v3
c = distBetween v3 v1
s = 0.5 * (a + b + c)
in sqrt (s * (s - a) * (s - b) * (s - c))
sqrt is Haskell's square root function.
Also, note that more than one equation is allowed in a let (or where) expression. The first characters of each equation, however, must line up vertically, and if an equation takes more than one line then the subsequent lines must be to the right of the first characters. For example, this is legal:
let a = aLongName
+ anEvenLongerName
b = 56
in ...
but neither of these is:
let a = aLongName
+ anEvenLongerName
b = 56
in ...
let a = aLongName
+ anEvenLongerName
b = 56
in ...
(The second line of the first example is too far to the left, as is the third line in the second
example.)
Although this rule, called the layout rule, may seem a bit ad hoc, it avoids the use of special syntax
to denote the end of one equation and the beginning of the next, thus enhancing readability. In practice, use of layout is rather intuitive. Just
remember two things:
1. The first character following either where or let (and a few other keywords that we will see later) is what determines the starting column for the
set of equations. Thus, we can begin the equations on the same line as the keyword, the next line, or whatever.
2. Be sure that the starting column is further to the right than the starting column associated with any immediately surrounding
clause (otherwise it would be ambiguous). The “termination” of an equation happens when something appears at or to the left of the starting column associated with that
equation.
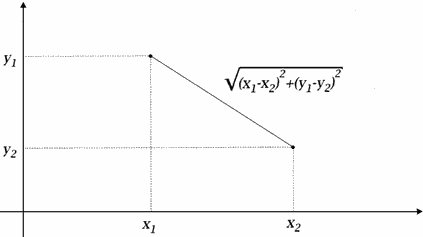
distBetween :: Vertex -> Vertex -> Float
distBetween (x1, y1) (x2, y2)
= sqrt ((x1 - x2)^2 + (y1 - y2)^2)
This definition is easy to see as an application of Pythagorean's theorem, as shown graphically in Fig. 2.2.
In summary, by collecting the four equations for area, we see that we have covered each of the constructors in the Shape data type:
area :: Shape -> Float
area (Rectangle s1 s2) = s1 * s2
area (RtTriangle s1 s2) = s1 * s2 / 2
area (Ellipse r1 r2) = pi * r1 * r2
area (Polygon (v1 : vs)) = polyArea vs
where polyArea :: [Vertex] -> Float
polyArea (v2 : v3 : vs') = triArea v1 v2 v3
+ polyArea (v3 : vs')
polyArea _ = 0
We can also prove properties about our functions, subject to the limitations of reasoning with floating-point numbers discussed in Section 1.6. For example, it would be nice if area (circle r) yielded the same result as circleArea r, where circleArea was defined in Section 1.4.2. We can do this easily by calculation:
area (circle r)
=> { unfold circle }
area (Ellipse r r)
=> { unfold area }
pi * r * r
=> { fold (^) }
pi * r^2
=> { fold circleArea } circleArea r
We can also prove more complex properties, such as:
area (RtTriangle s1 s2) ==> area (Polygon [(0, 0), (s1, 0), (0, s2)])
To prove this particular property it's more natural to start with the right-hand side and work backwards:
area (Polygon [(0, 0), (s1, 0), (0, s2)])
=> polyArea [(0, 0), (s1, 0), (0, s2)]
=> triArea (0, 0) (s1, 0) (0, s2) + polyArea [(0, 0), (0, s2)]
=> triArea (0, 0) (s1, 0) (0, s2) + 0
=> let a = distBetween (0, 0) (s1, 0)
b = distBetween (s1, 0) (0, s2)
c = distBetween (0, s2) (0, 0)
s = 0.5 * (a + b + c)
in sqrt (s * (s - a) * (s - b) * (s - c))
=> let b = sqrt (s1^2 + s2^2)
s = 0.5 * (s1 + b + s2)
in sqrt (s * (s - s1) * (s - b) * (s - s2)) -- (1)
We can simplify this further in two steps. First note:
s * (s - b) => 0.5 * (s1 + b + s2) * (0.5 * (s1 + b + s2) - b) => 0.5 * (s1 + b + s2) * (0.5 * (s1 - b + s2)) => 0.25 * (s1 + s2 + b) * (s1 + s2 - b) => 0.25 * ((s1 + s2)^2 - b^2) => 0.25 * ((s1 + s2)^2 - (s1^2 + s2^2)) => 0.25 * (s1^2 + 2 * s1 * s2 + s2^2 - (s1^2 + s2^2)) => 0.25 * (2 * s1 * s2) => 0.5 * s1 * s2
And further note:
(s - s1) * (s - s2) => (0.5 * (s1 + b + s2) - s1) * (0.5 * (s1 + b + s2) - s2) => 0.5 * (b - s1 + s2) * (0.5 * (b + s1 - s2)) => 0.25 * (b^2 - (s1 - s2)^2) => 0.25 * ((s1^2 + s2^2) - (s1 - s2)^2) => 0.25 * ((s1^2 + s2^2) - (s1^2 - 2 * s1 * s2 + s2^2)) => 0.5 * s1 * s2
Combining these and continuing from point (1), we get:
sqrt (s * (s - s1) * (s - b) * (s - s2)) => sqrt ((0.5 * s1 * s2) * (0.5 * s1 * s2)) => 0.5 * s1 * s2 => area (RtTriangle s1 s2)and we are done.
That was a lot of work! The primary reason for this is that Heron's general formula for the area of a triangle is subtle - and
powerful. It is interesting to note, however, that if we were to carry out this proof in mathematics, we would reason in a very similar way, as follows. By Heron's formula, the area of
a polygon with vertices (0, 0), (s1, 0) and (0, s2) is given
as follows:
Let
s = ½(a + b + c),
a = |(0, 0), (s1, 0)|,
b = |(s1, 0), (0, s2)|,
c = |(0, s2), (0, 0)|
(where | p1, p2| is the distance between vertices p1 and p2). Then the area is given by:
√s(s - a)(s - b)(s - c).
Simplifying a to s1 and c to s2 yields:
√s(s - s1)(s - b)(s - s2) (2.1)
where b = √s12 + s22
and s = ½ (s1 + b + s2).
We can simplify this further in two steps. First note:
s(s - b) = ½ (s1 + b + s2) (½ (s1 - b + s2))
= ¼ (s1 + s2 + b) (s1 + s2 - b) = ¼ ((s1 + s2)2 - b2)
= ¼ ((s1 + s2)2 - (s12 + s22)) = ¼ (s1 + 2s1 s2 + s22 - (s12 + s22))
= ¼ (2s1 s2) = ½ s1 s2
And further note:
(s - s1) (s - s2) = ½ (b - s1 + s2) (½ (b + s1 - s2))
= ¼ (b2 - (s1 - s2)2) = ¼ ((s12 + s22) - (s1 - s2)2)
= ¼ ((s12 + s22) - (s12 - 2s1 s2 + s22))
= ½ s1 s2 Combining these and continuing from point (1), we get:
√s(s - s1)(s - b)(s - s2)
= √(½ s1 s2) (½ s1 s2)
= ½ s1 s2
This last formula is just the area of a right triangle with sides s1 and s2. If you compare this mathematical proof with the corresponding proof by calculation in Haskell, you will find that they are almost identical, except for the notation used. So reasoning in Haskell is very often quite the same as reasoning in mathematics. Because we often use mathematics to specify the correct behavior of our programs, a proof by calculation in Haskell is a proof both about the implementation and about the specification. This is why Haskell is sometimes referred to as an “executable specification language”.
Unfortunately, as discussed in Section 1.6, care must be taken when performing this kind of reasoning with floating-point numbers. As is often the case, numbers that do not approach the limits of floating-point precision work perfectly well:
area (RtTriangle 3.652 5.126) ==> 9.36008 area (Polygon [(0, 0), (3.652, 0), (0, 5.126)]) ==> 9.36008whereas ones that do can yield inconsistent results:
area (RtTriangle 0.0001 5.126) ==> 0.0002563 area (Polygon [(0, 0), (0.0001, 0), (0, 5.126)]) ==> 0.000256648
 Exercise 2.3
Exercise 2.3Prove the following property:
area (Rectangle s1 s2) ==> area (Polygon [(0, 0), (s1, 0), (s1, s2), (0, s2)])
 Exercise 2.4
Exercise 2.4Define a function convex :: Shape -> Bool that determines whether or not its argument is a convex shape (although we are mainly interested in the convexity of polygons, you might as well define it for each kind of shape).
 Exercise 2.5
Exercise 2.5Here is an alternative way to compute the area of a polygon. Consider a polygon in quadrant 1 of the Cartesian plane (i.e., every vertex has positive x and y coordinates). Then every pair of adjacent vertices forms a trapezoid with respect to the x-axis. Starting at any vertex and working clockwise, compute these areas one-by-one, counting the area as positive if the x-coordinate increases, and negative if it decreases. The sum of these areas is then the area of the polygon.
It is easy to see that this algorithm is correct for a convex polygon by just looking at an example, as in Fig. 2.3. But the real beauty in this algorithm is that it works for concave polygons as well (see figure), and for a polygon located anywhere in the Cartesian plane. It is also more efficient than our previous algorithm. (Why?)
Write a Haskell function to compute polygonal areas in this way.
(Note: Polygons can not only be convex or concave, but also self-crossing. Consider, for example, the four-vertex polygon that outlines a “bowtie”, or the five-vertex polygon that outlines a five-pointed star. What is the proper notion of area in this case, and do any of the algorithms discussed here compute it properly?)
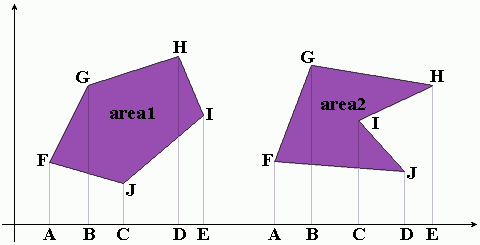
area2 = AFGB + BGHE - CIHE + CIJD - AFJD
Figure 2.3. Using Trapezoids to Compute Area of Polygon
Recall the discussion at the beginning of this chapter about modules and the desire to make visible only those named values that are of interest to the user of a module, thereby hiding irrelevant details of the implementation. We can now fill in the module declaration details to achieve this effect:
module Shape (Shape (Rectangle, Ellipse, RtTriangle, Polygon),
Radius, Side, Vertex,
square, circle, distBetween, area
) where
...
The list of names above are those entities that are intended to be visible, or exported, from the module. These names come in
three flavors:
1. Data types (in this case the data type Shape) that are listed with their constructors in parentheses.
A data type and its list of constructors may be abbreviated by just listing the name of the data type followed by (...). For example, the entire Shape data type may be exported using the form Shape (...). There are many other rules concerning the import and export of entities to and from modules. Some of these rules will be used later in the text, but you should consult the Haskell report for all of the details.
3. Ordinary values (in this case the functions square, circle, distBetween and area).
So, for example, the function triArea is not exported from the Shape module, and thus is not available for use by someone importing the module.
It is sometimes desirable to export everything from a module. A shorthand way to express this is to simply write:
module Shape where ...(i.e., omitting the list of exports is equivalent to exporting everything).